
Photo by Kimberly Farmer on Unsplash
A Simple Explanation of Consistent Hashing: From background to how it is an efficient tool for Data Distribution
In a distributed system, data is often partitioned across multiple nodes to achieve horizontal scalability and fault tolerance. Each node is responsible for storing and managing only a subset of the data.
To distribute data across an N-server cluster, a common approach is to balance the data load using a simple hash method. The method involves using a hash function to determine which server in the cluster the data should be assigned to.
ServerNumber = hash(dataKey)%N, where N is the total number of servers in your cluster
let's consider an example with N = 4 servers and 8 string keys. In the following table, we have computed the hash values for each key and assigned them to a server by taking the modulus of their hash value with 4, which is the total number of servers in the cluster
| Data Key | Hash Value | Server Number - (hash value %4) |
| key0 | 11 | 3 |
| key1 | 3 | 3 |
| key2 | 14 | 2 |
| key3 | 6 | 2 |
| key4 | 9 | 1 |
| key5 | 1 | 1 |
| key6 | 12 | 0 |
| key7 | 4 | 0 |
And to retrieve the server where a specific key is stored, we use the same modular operation hash(key) % 4. For example, if we apply the hash function to key0 and get a hash value of 11, then we can determine that the corresponding server is 3 .
So far so good, this approach looks perfect and it works well. However, the problem arises when a new server is added or an existing server is removed.
For instance, if a server goes offline (let's say server 1 in our example), the size of the server pool is reduced to 3. When we apply the same hash function to a key, we get the same hash value as before. However, when we apply the modular operation with a different number of servers(now 3), we get a different server index. This means that when server 1 goes offline, most clients will connect to the wrong servers to fetch data. The same table with 3 servers looks like this
| Data Key | Hash Value | Server Number - (hash value %3) |
| key0 | 11 | 2 |
| key1 | 3 | 0 |
| key2 | 14 | 2 |
| key3 | 6 | 0 |
| key4 | 9 | 0 |
| key5 | 1 | 1 |
| key6 | 12 | 0 |
| key7 | 4 | 1 |
And to solve this we have to redistribute all the data stored on all the servers again with a new formula hash(dataKey) %3 . This is a problem, isn't it? as its time and resource intensive. The problem is called Rehashing Problem.
And to mitigate this problem Consistent hashing mechanism is used
Consistent hashing
As per Wiki, "consistent hashing is a special kind of hashing technique such that when a hash table is resized, only n/m keys need to be remapped on average where n is the number of keys and m is the number of slots. In contrast, in most traditional hash tables, a change in the number of array slots causes nearly all keys to be remapped because the mapping between the keys and the slots is defined by a modular operation"
Let's deep dive into its working - The Algorithm behind
Hash space and hash ring
Assume SHA-1 is used as a hash function(f) and the output range of the hash function goes from X0, X1, X2, X3, ....., Xn. The actual SHA-1 cryptography space goes from 0 to 2^160-1 which means our X0 is 0 and Xn is 2^163-1.

By joining both ends, we get the hash ring
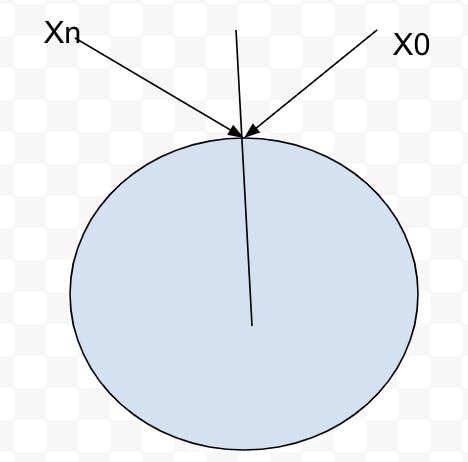
In this ring, we are going to map our server first as below
Hash servers: Using the same hash function f, we map servers onto the same hash ring created. After that, It looks like this.
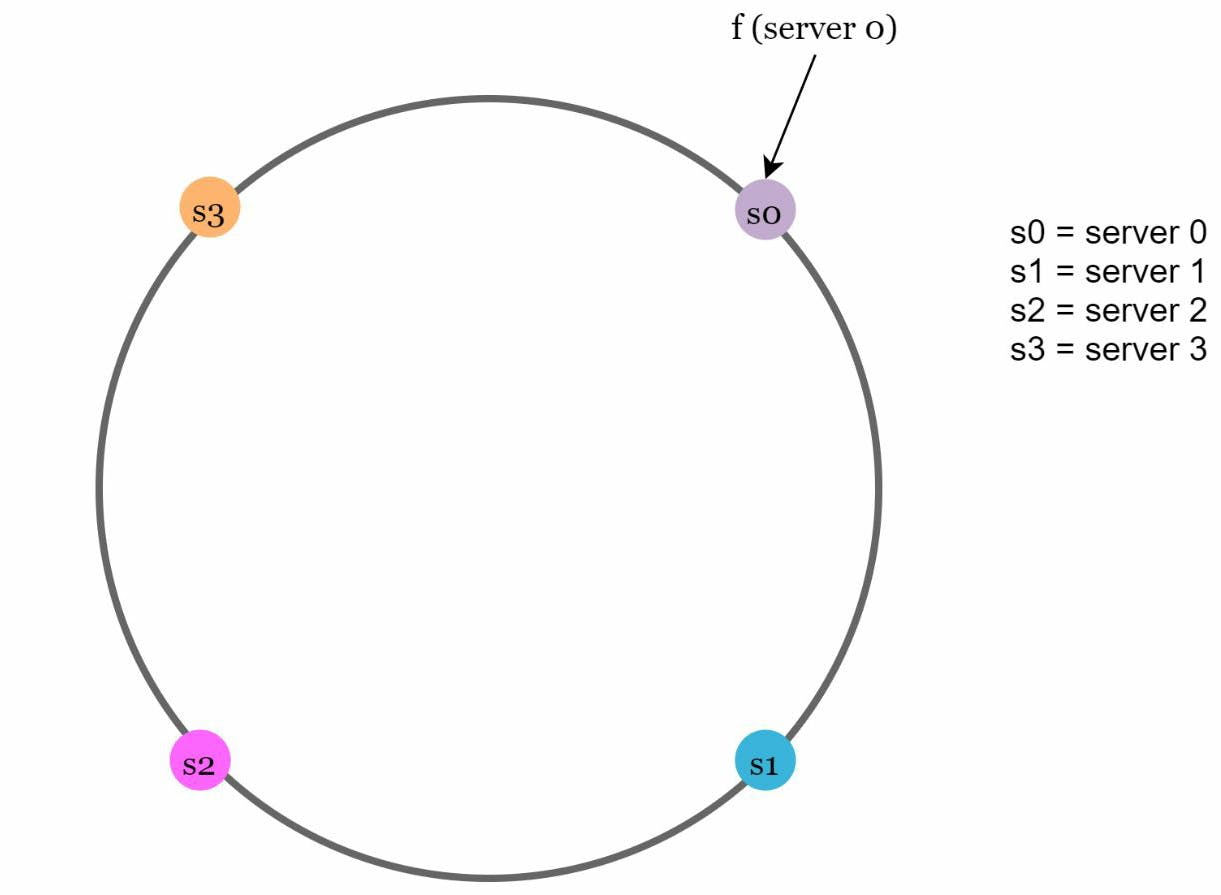
After mapping the servers let's map a few example input data keys using the same hash function f(sha1). After mapping the key in this ring it looks like
k0 , k1, k2, and k3 are keys
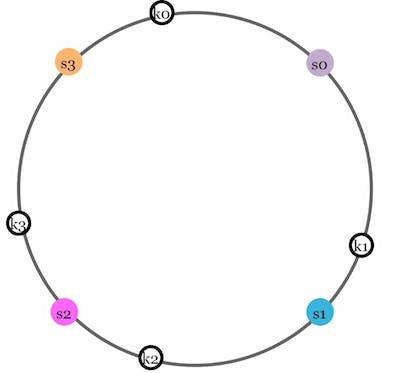
To store these keys on the server we go clockwise direction from the key location until a server is found and that is the destination server to store the keys. This is also called Server lookup.
This is what our ring looks like after storing keys to the servers.
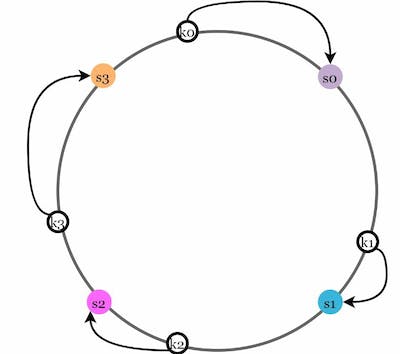
To summarise, we created a circular hash ring of a fixed size and mapped each server to a point on the ring using the same hash function(sha-1 in our case). To store data, a hash value is generated for the data which represents a location on the ring. Moving clockwise from that location, the first server encountered is assigned to store the data.
Let's discuss now what happens when we remove a server or add a server
Add a Server
Using the logic described above, let's say a new server 4(S4) is added. If a new server is added only key0 needs to be redistributed. k1, k2, and K3 remain on the same servers. So before server 4 is added, key0 is stored on server 0. Now, key0 will be stored on server 4 because server 4 is the first server it encounters by going clockwise from key0’s position on the ring.
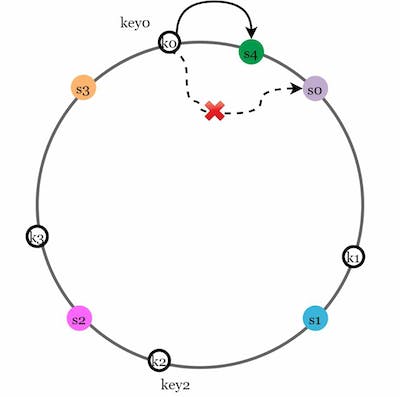
Remove a server
Removing the server from the ring requires the redistribution of a small number of keys which is only the keys located on that server.
In the above example if we remove the server S1, only the key k1 is needed to relocate and other keys remain on their server. The new destination of the key k1 will be the next available server in a clockwise direction which is s2
With this consistent hashing approach we can see that when a node is added or removed from the network, only a portion of the data needs to be moved, and the rest of the data remains on the same nodes compared to traditional hashing data distribution technique
I hope you could understand the concept of Consistent hashing.
But.. but..., could there be a challenge to this? Yes, you guessed it right.
There is a possibility of non-uniform data distribution as it may be possible that a significant portion of the data goes to a particular server. This is a classic case of a "Hot spot Problem" (more on this problem and scenarios... in some other blog)
How to handle it then?
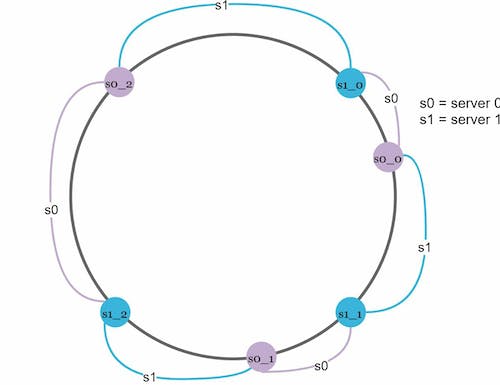
To handle this challenge we create virtual server nodes on the ring. They represent real server nodes and each real server can be represented by multiple virtual nodes
Let's see through a quick example. Consider having two servers S0, and S1. In the ring, we create more servers onto the ring for S0 as S0_0, S0_1, S0_2, and similarly for S1, so the data distribution uniformity can be increased.
That's a wrap!
References:
Your engagements are welcome! I write about my learning of scalable system design concepts. Subscribe for more such articles.
